This blog post is based on the HackerRank Interview Preparation Kit array New Year Chaos problem. HackerRank provides programming challenges that can be solved in the web browser in a variety of programming languages, and give real-time feedback on your solution’s success.
This solution solves for a 100% score!
HackerRank Problem – New Year Chaos
It is New Year’s Day and people are in line for the Wonderland rollercoaster ride. Each person wears a sticker indicating their initial position in the queue from 1 to n. Any person can bribe the person directly in front of them to swap positions, but they still wear their original sticker. One person can bribe at most two others.
Determine the minimum number of bribes that took place to get to a given queue order. Print the number of bribes, or, if anyone has bribed more than two people, print Too chaotic.
Example
q = [1,2,3,5,4,6,7,8]
If person 5 bribes person 4, the queue will look like this: 1,2,3,4,5,6,7,8. Only 1 bribe is required. Print 1.
q = [4,1,2,3]
Person 4 had to bribe 3 people to get to the current position. Print Too chaotic.
Function Description
Complete the function minimumBribes in the editor below.
minimumBribes has the following parameter(s):
- int q[n]: the positions of the people after all bribes
Returns
- No value is returned. Print the minimum number of bribes necessary or
Too chaoticif someone has bribed more than 2 people.
Input Format
The first line contains an integer t, the number of test cases.
Each of the next t pairs of lines are as follows:
– The first line contains an integer t, the number of people in the queue
– The second line has n space-separated integers describing the final state of the queue.
Constraints
1 <= t <= 101 <= n <= 10^5
Subtasks
For 60% score 1 <= n <= 10^3
For 100% score 1 <= n <= 10^5
New Year Chaos HackerRank Samples
Sample Input
STDIN Function ----- -------- 2 t = 2 5 n = 5 2 1 5 3 4 q = [2, 1, 5, 3, 4] 5 n = 5 2 5 1 3 4 q = [2, 5, 1, 3, 4]
Sample Output
3 Too chaotic
Explanation
Test Case 1
The initial state:

After person 5 moves one position ahead by bribing person 4:

Now person 5 moves another position ahead by bribing person 3:

And person 2 moves one position ahead by bribing person 1:

So the final state is 2,1,5,3,4 after three bribing operations.
Test Case 2
No person can bribe more than two people, yet it appears person 5 has done so. It is not possible to achieve the input state.
Key HackerRank Test PreRequisites
HackerRank practice questions may require pre-requisite knowledge to solve; they’re not all designed to be solved with your imagination. In this case, an understanding of sorting algorithms will be helpful.
This Medium article contains helpful GIFs that illustrate different sorting algorithms.
Spoiler: in this solution, we build a bubble sort algorithm and count the swaps needed to get an element into its correct position.
Exploring the HackerRank Constraints
Constraint 1
1 <= t <= 10 indicates that each “test” actually contains many test cases. Each test may have between 1 and 10 arrays of numbers that your algorithm must process.
Constraint 2
1 <= n <= 10^5 indicates that each test case array may have between 1 and 100,000 elements in it. This means a worst-case test scenario will have 10 tests, each with 100,000 elements in it.
Subtasks
When the subtasks talk about passing at 60% and 100% based on the second constraint, we have a dead giveaway: some test cases will fail in a suboptimal solution due to timeouts. This means that you will need to carefully consider how many times you are iterating over the provided collection, as doing this unnecessarily will fail to meet the 10^5 performance expectations.
When a test fails due to a timeout, it will tell you explicitly in the output window, as below:
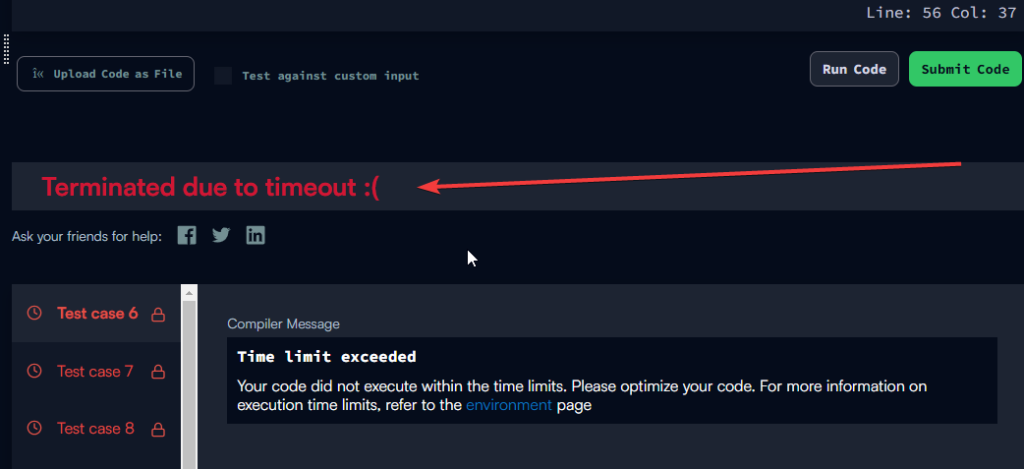
I tend to find that it becomes much less stressful to draft out an algorithm that is functionally correct and then optimise it later. It’s much easier to step back from a solid foundation and iterate, than it is to continue learning about the problem on the spot, and wrestling with non-functional requirements on top. It also gives you a nice confidence boost to know that you’re making progress!
Assumptions
When I first read this challenge, I became worried. My mind started racing about the possible permutations and combinations of orders that the bribes could happen. For example, what happens if person 2 bribes before person 3, but then person 3 bribes after them? That could push person 1 all the way to the back of the queue if every person did this in ascending order…
In order to start building something, I placed my bets on the assumption that bribes could only take place from the back of the queue to the front. This was the case in all of the examples given. I.e. “If person 5 bribes person 4”, “Person 4 had to bribe 3 people”, and in the images for the test cases, person 5 bribed to their position, followed by person 2.
Given the rigidity of this assumption, we can effectively see people bubbling up from the back of the array, swapping with only the next lowest-value person to their left. To achieve this solution, we need to do the exact opposite, which means we will perform a bubble sort in ascending order on the collection (with some added checks and optimisations thrown in)!
HackerRank New Year Chaos 60% Solution
With all of the pre-requisites and assumptions understood, let’s take a look at a 60% solution to start. This is where I ended up on my first iteration of the solution.
public static void minimumBribes(List<int> q)
{
// Keep track of each person's moves based on their original position - it's like their ID
// This will be used to validate their moves and terminate with "too chaotic"
var moves = new Dictionary<int, int>();
// Keep a separate tracker of the total moves, so we don't have to sum all
// of the dictionary moves at the end
var totalMoves = 0;
// This controls the outer loop - we need to iterate the collection an unknown number of times
var continueScanning = true;
while (continueScanning)
{
continueScanning = false;
for (int i = 1; i < q.Count(); i ++)
{
var currentValue = q[i];
var previousValue = q[i-1];
if (currentValue < previousValue)
{
if (moves.TryGetValue(previousValue, out var currentCount))
{
if (currentCount == 2)
{
Console.WriteLine("Too chaotic");
return;
}
moves[previousValue]++;
}
else
{
moves[previousValue] = 1;
}
totalMoves++;
q[i] = previousValue;
q[i-1] = currentValue;
continueScanning = true;
break;
}
}
}
Console.WriteLine(totalMoves);
}
Setting Up the Bubble Sort Loop
// This controls the outer loop - we need to iterate the collection an unknown number of times
var continueScanning = true;
while (continueScanning)
{
continueScanning = false;
for (int i = 1; i < q.Count(); i ++)
{
The bubble sort is orchestrated in two loops.
The inner loop in this solution starts scanning from the second element of the collection until the end. This is an important detail, as this implementation will look back and compare the prior element to the current one. While it is possible to do a bubble sort looking forward, you then need to adjust the loop condition so as to avoid an out of bounds exception.
In this loop if we perform a swap, we exit the loop so that we can start again, because a bubble sort is only finished if we can scan the collection and not perform a swap.
The outer loop, which is controlled by a boolean flag allows us to iterate the collection many times. The first line of the loop continueScanning = false; sets up a termination condition – if no swaps are performed we can exit.
Let’s zoom into the bubble sort swapping logic to start with.
Bubble Sort Swapping Logic
var currentValue = q[i];
var previousValue = q[i-1];
if (currentValue < previousValue)
{
...
totalMoves++;
q[i] = previousValue;
q[i-1] = currentValue;
continueScanning = true;
break;
}
We look at the current value and compare it to the prior value. In the very first iteration of this loop, currentValue will be element 2 of the collection, and previousValue will be element 1.
If the current value is smaller than the element before it, then we need to swap them, as we are sorting the collection in ascending order. In this case, we count this swap as a totalMove, swap the elements, and tell our outer loop that we need to iterate the collection again. We failed to iterate the collection without performing a swap, so we can’t be sure it’s completely sorted. Finally, we break out of the inner loop.
At this point, we have enough logic to cater for happy-path tests. I.e. tests that do not need to return too chaotic.
The Unhappy Path: Too Chaotic
// Keep track of each person's moves based on their original position - it's like their ID
// This will be used to validate their moves and terminate with "too chaotic"
var moves = new Dictionary<int, int>();
...
while (continueScanning)
{
continueScanning = false;
for (int i = 1; i < q.Count(); i ++)
{
var currentValue = q[i];
var previousValue = q[i-1];
if (currentValue < previousValue)
{
if (moves.TryGetValue(previousValue, out var currentCount))
{
if (currentCount == 2)
{
Console.WriteLine("Too chaotic");
return;
}
moves[previousValue]++;
}
else
{
moves[previousValue] = 1;
}
...
}
}
}
The question tells us that no single person can bribe more than 2 times. This means that we need a way of keeping track of a counter against each person.
We define a dictionary called moves for this, with an integer key. This is the person’s original position, as it is unique to them. The integer value represents the total moves that the person has made.
If we find that our elements are out of order, then we need to increment the bribe counter of the previousValue person. This person is currently out of order because they performed a bribe to get in front of our current person; we’re now reversing this. Think “Your bribe is being undone, so your counter is being increased”.
The logic itself is simple. If we have not counted a move for this person before, we initialise their key in the dictionary with the value 1. If we have counted for them before, we check if they have already moved twice. If so, we log Too chaotic and return from the method, otherwise we increment their counter.
Completing 60% Coverage by Recording our Happy Path Total Bribes Count
Console.WriteLine(totalMoves);
It’s a bit odd to log the result rather than return it from the method. Needless to say, at this point in the code we have an integer value ready and waiting, so we write it to the console.
At this point all test cases will pass except for 6, 7, 8 and 9.
HackerRank New Year Chaos 100% Solution
In order to get test cases 6, 7, 8 and 9 passing, we need to optimise how we iterate over the collection.
public static void minimumBribes(List<int> q)
{
// Keep track of each person's moves based on their original position - it's like their ID
// This will be used to validate their moves and terminate with "too chaotic"
var moves = new Dictionary<int, int>();
// Keep a separate tracker of the total moves, so we don't have to sum all
// of the dictionary moves at the end
var totalMoves = 0;
// This controls the outer loop - we need to iterate the collection an unknown number of times
var continueScanning = true;
// A tracker for where we will start searching in the collection
// Helps to optimise for 1 <= n < 10^5 case
var startingIndex = 1;
while (continueScanning)
{
continueScanning = false;
for (int i = startingIndex; i < q.Count(); i ++)
{
var currentValue = q[i];
var previousValue = q[i-1];
// Optimisation:
// The previous element's number matches its position (1 based index)
// This means that we never have to look at it again
// Start our next loop from the next position across so we keep iterating fewer elements
if (previousValue == i)
{
startingIndex = i + 1;
continue;
}
if (currentValue < previousValue)
{
if (moves.TryGetValue(previousValue, out var currentCount))
{
if (currentCount == 2)
{
Console.WriteLine("Too chaotic");
return;
}
moves[previousValue]++;
}
else
{
moves[previousValue] = 1;
}
totalMoves++;
q[i] = previousValue;
q[i-1] = currentValue;
continueScanning = true;
break;
}
}
}
Console.WriteLine(totalMoves);
}
Let’s look at the specific adjustments made.
Optimising the Inner Loop
public static void minimumBribes(List<int> q)
{
...
// A tracker for where we will start searching in the collection
// Helps to optimise for 1 <= n < 10^5 case
var startingIndex = 1;
while (continueScanning)
{
continueScanning = false;
for (int i = startingIndex; i < q.Count(); i ++)
{
...
// Optimisation:
// The previous element's number matches its position (1 based index)
// This means that we never have to look at it again
// Start our next loop from the next position across so we keep iterating fewer elements
if (previousValue == i)
{
startingIndex = i + 1;
continue;
}
...
}
}
}
The problem with the old algorithm is that each time we perform a swap, we start from the beginning of the collection again. This is wasteful because as we swap elements, they will eventually fall into the correct place.
For this specific HackerRank test, we know if a person is in the correct sorted place because the number that identifies them tells us this! It is the 1-based position that they started from.
Therefore, the first step we need to perform in our bubble sort loop is to check if the previous person we are bubbling against is already in the correct position. In this case, we can just compare their number against i. While i is a zero-based index of the current person, it can be used to represent the 1-based position of the previous person.
If the previous person is in the correct place, then we capture our new startingIndex as the position after our current person, which will mean the next iteration of the loop checks if they are in the correct place. We can just continue from this point as we don’t need to perform a swap check or break the loop, just i ++.
That’s it! This optimises the iterations of the bubble sort to pass the remaining performance-based tests.
Sloth Summary
Phew! This HackerRank challenge started out looking like a complex mess. However, as we stepped back from the question and thought critically about each of the statements made in the question, we were able to incrementally build a solution that eventually passed 100% of the test cases.
Ugly, hard-coded values are absolutely great examples of Sloth Code in HackerRank questions. Use them to ground your understanding of the problem and iterate to a more dynamic solution, only if the question requires it.
Happy Code Slothing! 🦥

